M1 BBS Graphes TP Dessin et Introduction iGraph
From silico.biotoul.fr
Contents |
Utilisation de la bibliothèque iGraph sous R
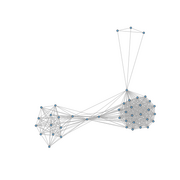
Pour cela nous allons travailler avec le graphe ci-contre dans lequel les sommets correspondent à des gènes de différents organismes procaryotes et les liens correspondent à une relation d'isorthologie inférée entre les gènes.
Fichiers au format edgelist :
- Media:Cleandb_Luca_1_S_1_1_65_Iso_Tr_1-CC1.gr (comporte les étiquettes des sommets)
- Media:Cleandb_Luca_1_S_1_1_65_Iso_Tr_1-CC1.tgr (le même mais les sommets sont numérotés)
Premiers pas
La librairie iGraph met à disposition tout un ensemble de fonctions pour le traitement et la visualisation de graphes. Nous allons utiliser aujourd'hui son interfaçage avec R. Pour la charger :
library(igraph)
Pour charger un graphe (différents format possibles : pajek, newick, ...) :
g = read.graph("http://silico.biotoul.fr/site/images/9/9f/Cleandb_Luca_1_S_1_1_65_Iso_Tr_1-CC1.tgr", directed=FALSE)
Consulter l'aide de la fonction (?read.graph) pour voir les autres formats supportés.
Pour l'afficher, il faut au préalable en effectuer le dessin (layout) :
# soit en une ligne en passant la fonction de dessin : plot(g, layout=layout.fruchterman.reingold) # soit en sauvegardant ce layout dans une variable : g.FR = layout.fruchterman.reingold(g) plot(g, layout=g.FR, vertex.size=3, vertex.label=NA)
Consulter l'aide des fonction plot.igraph et layout.fructhterman.reingold pour voir les options ainsi que les autres algorithmes de dessin disponibles.
Vous trouverez la documentation de la librairie sur le site dédié. Pour celle de l'interface R en ligne : http://igraph.org/r/
- Pour obtenir la liste des sommets : V(g)
- la liste des arêtes : E(g)
- Quel est l'ordre du graphe ? Combien a-t-il d'arêtes ?
On peut assigner des étiquettes aux sommets : V(g)$name = vector_of_labels
Remarque : la librairie étant codée en C puis interfacée avec R, cela créé au moins un petit inconvénient : les indices en C vont de 0 à n-1 alors que en R ils vont de 1 à n.
Charger les étiquettes des sommets :
V(g)$name=as.character(read.table("http://silico.biotoul.fr/site/images/6/61/Cleandb_Luca_1_S_1_1_65_Iso_Tr_1-CC1.cod")[,2]) plot(g, layout=g.FR, vertex.size=3, vertex.label=V(g)$name)
Les paramètres de la fonction plot de igraph sont décrits dans la documentation.
Il est possible de stocker de l'information sur le graphe, les sommets et/ou les arêtes avec les fonctions dédiées :
vertex_attr(g, name="name") vertex_attr(g, name="name", index=10)
- Quel est le diamètre du graphe ?
- Lister les points d'articulation (articulation.points)
- Longueur moyenne des plus courts chemins (sans valuation) (average.path.length)
- Afficher sa représentation canonique (canonical.permutation) et la matrice d'adjacence correspondante
- Lister les cliques maximales (maximal.cliques)
- Lister les composantes connexes (clusters) avant et après suppression du point d'articulation
- Parcours en largeur et en profondeur (graph.bfs et graph.dfs)
- Obtenir le line graph (line.graph)
- Arbre couvrant de poids minimum (minimum.spanning.tree)
- Plus courts chemins : utiliser les fonctions shortest.paths et get.shortest.paths pour obtenir la longueur des plus courts chemin entre tous les sommets, ainsi que le plus court chemin entre les sommets BantA01.AAP27658.1 et HmarA01.YUFN.
- la betweenness d'une arête est le nombre de plus courts chemins passant par cette arête. Utiliser la fonction edge.betweenness pour calculer cette valeur et l'ajouter au dessin.
Suppression du point d'articulation, extraction du sous graphe induit et affichage avant l'analyse des composantes connexes :
vids = which( V(g) != V(g)[ articulation.points(g) ]) # ou g1 = delete.vertices(g, articulation.points(g) ) g1.layout = g.FR[V(g) != V(g)[ articulation.points(g) ],] # pour conserver le même layout que g plot(g1, vertex.size=3, layout=g1.layout, vertex.label=V(g)$name, vertex.label.cex=.5) clusters(g1)
Partitionnement
Pour partitionner le graphe en communautés, différentes méthodes sont disponibles. Vous allez utilisez la betweenness des arêtes pour effectuer le partitionnement du graphe. Cette méthode sélectionne les arêtes dont la betweenness est la plus importantes afin de former des communautés (clusters).
Cette méthode ne fournit pas le meilleur partitionnement : seulement le clustering hiérarchique. Il va donc falloir déterminer où couper l'arbre pour former les clusters. Pour cela, il va falloir déterminer à quelle étape du clustering hiérarchique se situe le maximum de la mesure de qualité du partitionnement (on utilisera la modularité).
# community detection with edge-betweenness com = edge.betweenness.community(g) par(cex=.5) plot(as.dendrogram(com)) # find best partition com$best_step=0 com$best_modularity = -Inf for (i in 1:nrow(com$merges)) { ctm = cut_at(com, steps=i) mod = modularity(g, ctm) print(paste("step: ",i,", modularity:",mod)) if (mod>com$best_modularity) { com$best_step = i com$best_modularity = mod com$membership=ctm } } # plot best partition plot(g, layout=g.FR, vertex.color=com$membership, vertex.size=3, vertex.label=NA, main=paste("step",com$best_step,", modularity:",com$best_modularity))
High Dimensional Embedding
A présent, vous allez devoir implémenter l'algorithme de dessin HDE vu en cours puisqu'il n'est pas disponible dans iGraph.
On rappelle son principe :
- calculer les plus courts chemins entre chaque paire de sommets (utiliser la fonction shortest.paths(g))
- déterminer les sommets pivots
- le premier est pris au hasard
- les suivants sont sélectionnés l'un après l'autre en maximisant à chaque fois leur distance aux pivots déjà sélectionnés
- effectuer une ACP sur les coordonnées des sommets du graphes sur chacun des axes pivots
- effectuer la projection par rapport aux 2 ou 3 composantes principales
Sélection des pivots:
pivot_selection = function(g, n.pivots) { g.sp = shortest.paths(g) g.pivots = c( 1 ) g.others = 2:length(V(g)) while ( length(g.pivots) < n.pivots ) { p.new.i = 1 # index in g.others p.new.best.i = g.others[1] # intialize with index of first non pivot p.new.best.dist = 0 # iterate over non pivots (g.others) while ( p.new.i <= length(g.others) ) { p.new = g.others[ p.new.i ] p.new.dist = 0 for (p.old in g.pivots) { # add shortest path to each selected pivots p.new.dist = p.new.dist + g.sp[ p.old, p.new ] } # keep it if it maximizes distance if (p.new.dist > p.new.best.dist) { p.new.best.dist = p.new.dist p.new.best.i = p.new.i } p.new.i = p.new.i + 1 } # add best pivot to selected pivots g.pivots = c(g.pivots, g.others[p.new.best.i]) # remove best pivot from non pivots g.others = g.others[ -p.new.best.i ] } g.pivots }
Comparer le résultat obtenu par rapport à Fruchterman-Reingold sur le graphe précédent ainsi que sur une grille régulière de 10x10 générée avec la fonction suivante :
lat=graph.lattice(length=10,dim=2) # layout lat.FR=layout.fruchterman.reingold(lat) lat.HDE=layout.hde(lat) # tracé plot(lat, layout=lat.FR, vertex.size=3, vertex.label=NA) plot(lat, layout=lat.HDE, vertex.size=3, vertex.label=NA)
Augmenter la taille de la grille (par exemple 30), et apprécier le temps pris pour le dessin par l'algorithme de FR, et par HDE.
Disposant d'une matrice de distance, il également envisageable de faire du multidimensional scaling (cf. TD de Traitement de données biologiques sur les analyses multivariées) :
# MDS Layout layout.mds = function(g, ndim=2) { g.sp = shortest.paths(g) fit <- cmdscale(g.sp,eig=TRUE, k=ndim) # k est le nombre de dimensions fit$points[,1:ndim] } lat.MDS=layout.mds(lat) plot(lat, layout=lat.MDS, vertex.size=3, vertex.label=NA)
Avec HDE et MDS, on peut aussi dessiner le graphe en 3 dimensions :
# grille lat=graph.lattice(length=10,dim=2) lat.HDE=layout.hde(lat,ndim=3) rglplot(lat, layout=lat.HDE, vertex.size=3, vertex.label=NA) # cube lat=graph.lattice(length=6,dim=3) lat.HDE=layout.hde(lat,ndim=3) rglplot(lat, layout=lat.HDE, vertex.size=3, vertex.label=NA)
Dessin de graphes

Dans cette partie, nous allons voir comment lire/écrire un arbre au format Newick. Puis, comment afficher l'arborescence avec différents algorithmes :
- textuelle comme par exemple une arborescence de fichiers
- graphique
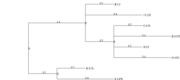
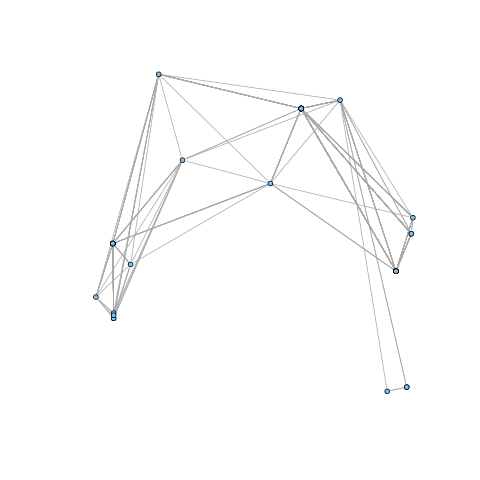
Pour cela, nous allons utiliser les arbres ci-contre.
Chargement d'un arbre au format Newick
La première étape consiste donc à pouvoir charger l'arbre au format Newick dans un script python.
Pour cela, vous pouvez compléter la librairie ci-dessous qui utilise la librairie que vous avez développée au cours des séances précédentes. manipuler les arbres :
#!/usr/bin/python3 # -*- coding: utf-8 -*- from pprint import pprint import Graph as gr def loadNewick(filename): def parseNewick(g, text): i=0 stack=[] idx=0 current = { 'parent': None, 'index': 0, 'id': 'root', 'length': 1.0 } nodes = [ current ] while i < len(text): if text[i]==' ': # skip spaces i+=1 if text[i]==';': # finished add root gr.addNode(g, current['id'], current) g['root'] = current['id'] i+=1 elif text[i]=='(': # new child idx += 1 N = { 'parent': current['index'], 'index': idx, 'id': idx, 'length': 1.0 } nodes.append(N) stack.insert(0, current['index']) current = N i+=1 elif text[i]==',': # end of label or branch length... next child incoming # create previous node gr.addNode(g, current['id'], current) parent = nodes[ stack[0] ] # parent is at the top of the stack idx += 1 N = { 'parent': parent['index'], 'index': idx, 'id': idx, 'length': 1.0 } nodes.append(N) current = N i+=1 elif text[i]==')': # new child complete gr.addNode(g, current['id'], current) current=nodes[ stack.pop(0) ] i+=1 elif text[i]==':': # incoming branch length # parse number nbText = '' i+=1 while text[i] in ['0','1','2','3','4','5','6','7','8','9','0','.','E','e','-']: nbText+=text[i] i+=1 current['length'] = float(nbText) else: # maybe incoming node label label='' while not text[i] in [' ',')',':',',',';']: label+=text[i] i+=1 current['id'] = label # all nodes created with correct label if provided, create edges for n in nodes: if n['parent'] is not None: gr.addEdge(g, nodes[ n['parent'] ]['id'], n['id'], { 'length': n['length']} ) n['parent'] = nodes[ n['parent'] ]['id'] # update parent id # clean up node attributes del n['index'] #del n['length'] # g = gr.createGraph(directed=True, weighted=True) g['weight_attribute'] = 'length' g['rooted'] = True with open(filename) as f: text = f.readline().rstrip() parseNewick(g,text) return g ##### main ##### if __name__ == "__main__": print('Tree lib tests') print("\n####") print(" # loadNewick('aTree.nwk')") t = loadNewick('aTree.nwk')
Affichage au format texte
Ajouter une fonction pour afficher un arbre sous forme d'arborescence de fichier. Le résultat pour toyExample devrait ressembler à ce qui suit :
|- A | |-0.4- F | | |-0.2- B | | |-0.4- J | | |-0.2- E | | | |-0.2- C | | | |-0.4- D | | | |-0.2- H | | | |-0.4- I | |-0.2- G | | |-0.2- K | | |-0.4- L
Écrire une procédure pour exporter l'arbre au format Newick.
Fructherman-Reingold
#!/usr/bin/python3 # -*- coding: utf-8 -*- from pprint import pprint import Graph as gr from math import sqrt from random import random def layoutFruchtermanReingold(g, nb_iterations=500, cool=1.0, max_displacement=10.0, width = 800, height=600): """ The force directed layout algorithm adapted from Fruchterman-Reingold, 1991. """ layoutFruchtermanReingoldInit(g, cool, max_displacement, width, height) for i in range(nb_iterations): layoutFruchtermanReingoldIteration(g) # remove temp attributes for n in g['nodes']: del g['nodes'][n]['force_x'] del g['nodes'][n]['force_y'] def layoutFruchtermanReingoldInit(g, cool=1.0, max_displacement=10.0, width = 800, height=600): """ Utility function (initialization) for the force directed layout algorithm adapted from Fruchterman-Reingold, 1991. """ k = sqrt(float(width)*height/g['nb_nodes'])/2 # optimal distance between 2 nodes fr = {} g['Fruchterman-Reingold'] = fr fr['k'] = k fr['cool'] = cool fr['canvas_width'] = width - 200 fr['canvas_height'] = height - 50 fr['max_displacement'] = max_displacement # initalize node positions for nid in g['nodes']: n = g['nodes'][nid] n['x'] = random()*float(width) n['y'] = random()*float(height) n['force_x'] = float(0) n['force_y'] = float(0) def layoutFruchtermanReingoldIteration(g): """ Utility function (an iteration for nodes displacements) for the force directed layout algorithm adapted from Fruchterman-Reingold, 1991. """ # calculate repulsive forces fr = g['Fruchterman-Reingold'] for v in g['nodes']: m = g['nodes'][v] m['force_x'] = float(0) m['force_y'] = float(0) for u in g['nodes']: n = g['nodes'][u] if u!=v: dx = m['x']-n['x'] dy = m['y']-n['y'] d = sqrt( dx**2 + dy**2 ) # avoid too small distances if d < 0.1: dx = 0.1 * random() + 0.1 dy = 0.1 * random() + 0.1 d = sqrt( dx**2 + dy**2 ) force = fr['k']**2/d m['force_x'] += force * dx / d m['force_y'] += force * dy / d # calculate attractive forces for u in g['nodes']: for v in g['edges'][u]: if u!=v: # do not process loops (division by 0) dx = g['nodes'][v]['x'] - g['nodes'][u]['x'] dy = g['nodes'][v]['y'] - g['nodes'][u]['y'] d = sqrt( dx**2 + dy**2 ) force = d**2 / fr['k'] g['nodes'][u]['force_x'] += force * dx / d g['nodes'][u]['force_y'] += force * dy / d g['nodes'][v]['force_x'] -= force * dx / d g['nodes'][v]['force_y'] -= force * dy / d # move nodes for n in g['nodes']: disp = sqrt( g['nodes'][n]['force_x']**2 + g['nodes'][n]['force_y']**2 ) if disp > fr['max_displacement']: scale = sqrt( fr['max_displacement']**2 / disp**2 ) g['nodes'][n]['force_x'] *= scale g['nodes'][n]['force_y'] *= scale g['nodes'][n]['x'] += g['nodes'][n]['force_x'] g['nodes'][n]['y'] += g['nodes'][n]['force_y'] g['nodes'][n]['x'] = min( fr['canvas_width'], max( 0, g['nodes'][n]['x'] ) ) g['nodes'][n]['y'] = min( fr['canvas_height'], max( 0, g['nodes'][n]['y'] ) ) # cooling fr['max_displacement'] *= fr['cool'] # SVG Rendering def renderSVG(g, filename=None, width=800, height=600): def svgText(x,y,text): return '<text x="'+str(x+20)+'" y="'+str(y+20)+'">'+text+"</text>\n" def svgLine(x1,y1,x2,y2): return '<line x1="'+str(x1+20)+'" y1="'+str(y1+20)+'" x2="'+str(x2+20)+'" y2="'+str(y2+20)+'" style="stroke:rgb(0,0,0);stroke-width:1"/>\n' def svgEdge(x1,y1,x2,y2): return '<path d="M'+str(x1+20)+','+str(y1+20)+' L'+str(x2+20)+','+str(y2+20)+'" style="stroke:rgb(0,0,0); stroke-width:1px; fill: none; marker-end: url(#markerArrow);"/>\n' def svgNode(x, y): return '<circle cx="'+str(x+20)+'" cy="'+str(y+20)+'" r="5" stroke="black" stroke-width="1" fill="white"/>' svg = '<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="'+str(width)+'" height="'+str(height)+'">\n' svg += '<defs>\n <marker id="markerArrow" markerWidth="13" markerHeight="13" refX="15" refY="6" orient="auto">\n <path d="M2,2 L2,10 L10,6 L2,2" style="fill: #000000;" />\n </marker>\n</defs>\n' svg += '<path d="M0,0 L'+str(width)+',0 L'+str(width)+','+str(height)+' L0,'+str(height)+' L0,0" style="fill: #eee;"/>' for ui in g['nodes']: u = g['nodes'][ui] for vi in g['edges'][ui]: v = g['nodes'][vi] svg += svgEdge( int(u['x']), int(u['y']), int(v['x']), int(v['y'])) for n in g['nodes']: svg += svgNode(g['nodes'][n]['x'], g['nodes'][n]['y']) svg += svgText( g['nodes'][n]['x']+10, g['nodes'][n]['y']+5, n) svg += '</svg>\n' if filename is None: print(svg) else: f = open(filename, 'w') f.write(svg) f.close() ##### main ##### if __name__ == "__main__": g=gr.loadSIF('dressing.sif') layoutFruchtermanReingold(g) pprint(g) print('#### SVG Rendering') renderSVG(g) renderSVG(g,'dressing.svg')
Installation de igraph en 2017
La version la plus récente installable sous linux est la 0.1.2 : https://cran.r-project.org/src/contrib/Archive/igraph/igraph_0.1.2.tar.gz
Malheureusement, cette version est complètement différente de la version actuelle et il n'est pas pédagogique d'apprendre à l'utiliser.
Pour installer cette version :
install.packages('https://cran.r-project.org/src/contrib/Archive/igraph/igraph_0.1.2.tar.gz')